A Proof of Lemma XIV of the First Book of Newton's Principia

September 2022

Lemma XIV The perpendicular, let fall from the focus of a parabola on its tangent, is a mean proportional between the distances of the focus from the point of contact, and from the principal vertex of the figure.

Newton's original argument is as follows:

For, let $AP$ be the parabola, $S$ its focus, $A$ its principal vertex, $P$ the point of contact, $PO$ an ordinate to the principal diameter, $PM$ the tangent meeting the principal diameter in $M$, and $SN$ the perpendicular from the focus on the tangent. Join $AN$, and because of the equal lines $MS$ and $SP$, $MN$ and $NP$, $MA$ and $AO$, the right lines $AN$, $OP$ will be parallel; and thence the triangle $SAN$ will be right-angled at $A$, and similar to the equal triangles $SNM$, $SNP$; therefore $PS$ is to $SN$ as $SN$ is to $SA$.

Though this might seem to be complete, upon further inspection it is clear that Newton has left quite a lot of work for us to do; as this argument relies on the equality of $MS$ and $SP$, $MN$ and $NP$, as well as the equality of $MA$ and $AO$. So if we wish to complete Newton's argument, we need to prove these identities. And so we need to prove the following propositions.

Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the distance between $M$ and the focus is equal to the distance between the focus and the point of tangency.
Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the perpendicular dropped from the focus onto the tangent is equidistant from $M$ and the point of tangency.
Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the distance between $M$ and the vertex is equal to the distance between the vertex and the perpendicular dropped from the point of tangency.

But before we get into this, let me give an introduction to dealing with parabolas geometrically for those who might not be familiar with such things.

Parabolas done geometrically

Most people know parabolas as curves traced by the functions of the form $f(x) = a[k(x-p)]^2 + q$ where $(p, q)$ is the vertex of the parabola. Though this representation of a parabola is very useful in a large variety of problems—notably those in classical mechanics—it is not a useful tool for our current problem. The equations get too unwieldy too quickly. Fortunately, one may also study parabolas from a geometric/synthetic perspective which is better suited to this task.

Definition 1 Given a line $d$ and a point $F$, a parabola is defined as the shape such that all points on the parabola are equidistant from $d$ and $F$. By convention we call the $d$ the directrix and $F$ the focus.

From this definition it is clear that the vertex of the parabola is the midpoint of the line connecting the focus and the directrix. If it is not clear, then you can prove it yourself by using the fact that the vertex is the point on the parabola which is closest to the directrix.

It might not be totally clear how this is related to the algebraic definition. But I'll convince you that these two definitions have all the same properties as each other. For instance, we know that a parabola $f$ with its vertex at $(0,0)$ is even; that is $f(-x) = f(x)$. The analogous property is stated geometrically as:

Theorem 1 In any parabola, the line passing through the vertex and the focus is the axis of symmetry. Meaning that if two points are equidistant from the line passing through the focus and the vertex, then they are equidistant from the directrix.

Trace a parabola with focus $F$ and a directrix through $A$ such that $AF$ is perpendicular to the directrix. Pick any point $X_1$ on the directrix and reflect it over $A$ at $X_2$. Notice that, since $X_1F = X_2F$, then $\angle FX_1A = \angle FX_2A$. And as $\angle Y_1X_1A$ and $\angle Y_2X_2A$ are right angles, then $\angle Y_1X_1F$ and $\angle Y_2X_2F$ are both equal to $90^\circ - \angle FX_1A$. We now use the defining property of the parabola by observing that $\triangle X_1Y_1F$ and $\triangle X_2Y_2F$ are both isosceles. And since two of their angles and two of their sides, namely $\angle Y_1X_1F$ and $\angle Y_2X_2F$ and $X_1F$ and $X_2F$ are equal, then $\triangle X_1Y_1F \cong \triangle X_2Y_2F$. Therefore it is clear that $Y_1X_1 = Y_2X_2$. $\blacksquare$

Now you might rightfully protest and say that this isn't enough. "There are many things other than parabolas which are symmetric", I hear you say. So now we'll try to convert this shape onto the Cartesian coordinate system to see whether these two definitions really are equivalent.

Theorem 2 Let the vertex of the parabola be placed at the origin and let the line $y=-1$ be the directrix. The function that traces this parabola is $y = ax^2$ for some $a$.

Since we determined that the vertex is the midpoint of the line connecting the focus with the axis of symmetry, then it should be clear that in our present construction the focus is $F = (0,1)$. Let $P = (x,y)$ be on the parabola. Then from our definition we know that $y + 1 = PF$ which is equal to $\sqrt{|x|^2 + |y-1|^2}$. So we obtain the equation $$ y + 1 = \sqrt{|x|^2 + |y-1|^2} $$ Which we intend to solve for $y$. So square both sides $$ y^2 + 2y + 1 = x^2 + y^2 - 2y + 1 $$ And by isolating for $y$ we obtain: $ y = \frac{1}{4}x^2 $. $\blacksquare$

By this point you should truly be convinced of the equality of these two definitions. And if not, then feel free to try Newton's lemma by using algebraic methods. Now I'll provide a sample problem to increase the reader's familiarity with using these techniques.

Exercise 1 Suppose that on a parabola with vertex $V$ and a focus $F$ there exists a point $A$ such that $AF = 20$ and $AV = 21$. What is the sum of all possible values of the length $FV$. (From the AMC 12)

Show solution

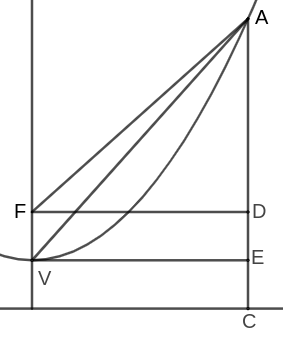
After drawing the figure described in the question, draw the directrix of the parabola and drop a perpendicular from $A$ onto the directrix at $C$. Let $x = FV$ and notice that $$AV^2 - (AC - x)^2 = AF^2 - (AC - 2x)^2$$ Now we can solve this equation for $x$. First we substitute the values of $AF$, $AV$, and since $AC = AF$ by the definition of the parabola, we substitute that as well. $$ 441 - (20 - x)^2 = 400 - (20 - 2x)^2 $$ By rearranging we obtain $$ \begin{aligned} 41 &= (20 - x)^2 - (20 - 2x)^2 \\ &= [(20 - x) + (20 - 2x)][(20 - x) - (20 - 2x)] \\ &= x(40 - 3x) \\ &= 40x - 3x^2 \end{aligned} $$ And so the solution to our problem is the sum of the two roots of the equation $-3x^2 + 40x - 41$. This is done easily via Vieta's formulas and more tediously via simply finding the roots. In the end the answer is $\frac{40}{3}$. Q.E.D.

Now let's show a really cool property of parabolas that we'll end up using later in our proof. The reflective property of the parabola! This result explains why parabolic mirrors work the way they do.

Theorem 3 In a parabola with a tangent at $P$, the angle made by the tangent and the parallel line to the axis of symmetry at $P$ is equal to the angle made by the line drawn from the focus to $P$ and the tangent.

I tried to prove this via synthetic methods, but I failed so here is an analytic proof for $y = x^2$ because I was too lazy to do the general version. Let $P$ be a point on the aforementioned parabola, so $P = (a, a^2)$ for some $a$. As such, slope of the tangent at $P$ is $2a$. For this parabola, the focus, $F$, is at point $(0, \frac{1}{4})$ and the intersection of the perpendicular from $P$ and the directrix is $(a, -\frac{1}{4})$. Therefore slope of $FD$ is $$ \frac{\frac{1}{4} - \frac{-1}{4}}{0 - a} = -\frac{1}{2a} $$ And since the slopes of $AC$ and the tangent at $P$ are negative reciprocals of each other, then they are perpendicular. And since $FP = PD$ and the tangent is perpendicular to $FD$, then the tangent bisects $FD$ and as such $\angle FPA = \angle DPA$. Which is what we wanted to show. Q.E.D.

Back to Newton

Previously I'd stated three goals that have to be achieved for this proof to be complete. Those being:

[ ] Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the distance between $M$ and the focus is equal to the distance between the focus and the point of tangency.
[ ] Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the perpendicular dropped from the focus onto the tangent is equidistant from $M$ and the point of tangency.
[ ] Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the distance between $M$ and the vertex is equal to the distance between the vertex and the perpendicular dropped from the point of tangency.

Now we'll go through these goals step by step and try to achieve them. À la means-ends analysis and GPS.

Goals 1, 2 Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the distance between $M$ and the focus is equal to the distance between the focus and the point of tangency and that the perpendicular dropped from the focus onto the tangent is equidistant from $M$ and the point of tangency.

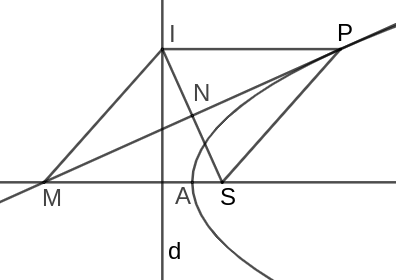Goals 1 and 2 Let $d$ be the directrix of our parabola $S$ be the focus, and $P$, be the point of tangency. As such, $SP = PI$ where $PI \perp d$. Let $N$ be a point on $MP$ such that $SN \perp MP$. Notice that by the reflective property, $\angle IPN = \angle SPN$. Therefore $\triangle PNI \cong \triangle PNS$ since they share $PN$. And since we said that $SN \perp MP$, then both $\angle INP$ and $\angle SNP$ are equal to $90^\circ$ making $I$, $N$ and $S$ collinear. This also implies that $SN = IN$.

We said that $IP \perp d$, this tells us $IP \parallel MS$, which also forms right angles with $d$. As such $\triangle MNS \cong \triangle IPN$ which in turn is congruent to $\triangle PNS$. Therefore, $MN = NP$ and $MS = SP$. Q.E.D.

Well this wasn't too bad. We've already achieved two of our three goals:

[X] Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the distance between $M$ and the focus is equal to the distance between the focus and the point of tangency.
[X] Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the perpendicular dropped from the focus onto the tangent is equidistant from $M$ and the point of tangency.

All we need to do now is to achieve the final goal and we'll be done.

Goal 3 Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the distance between $M$ and the vertex is equal to the distance between the vertex and the perpendicular dropped from the point of tangency.

Drop a perpendicular from $P$ to $O$. Notice that since $\angle PNS$ and $\angle POS$ are both right angles, then $NPOS$ is a cyclic quadrilateral. As such, $\angle SON = \angle NPS$ which is in turn equal to $\angle NSM$. ¹ It should be clear now that $MN = NO$.

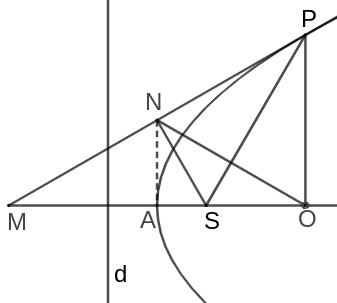
By this point the clear next step is to show that $\triangle MNA \cong \triangle NOA$. However, this is only possible if $NA \perp OM$. However, we don't know if this is true yet. Well whatever. We'll just assume it for now. As such, $\triangle MAN \cong \triangle NOA$ and so $MA = AO$. Q.E.D.

Well that's no good. We've technically ticked off goal three, but we've added another goal in its stead!

[X] Given that the tangent of a parabola intersects its axis of symmetry at $M$, then the distance between $M$ and the vertex is equal to the distance between the vertex and the perpendicular dropped from the point of tangency.
[ ] The perpendicular dropped from $N$ meets the axis of symmetry at the vertex.

Well we have nothing better to do so might as well try to finish the last goal.

Goal 4 The perpendicular dropped from $N$ meets the axis of symmetry at the vertex.

Back in goal 1 we showed that $\triangle PIN \cong \triangle PNS \cong \triangle MNS$ by using the reflective property of the parabola. This means that $PIMS$ is a rhombus. A consequence of this is that $IE = NA$ where $E$ is a point on $d$ such that $NE \perp IC$ and $A$ is a point on $MS$ such that $NA \perp MS$. By using goal 1 we may also deduce that $IN = NS$, as such $\triangle IEN \cong \triangle NAS$. Therefore $CA = EN = AS$, meaning that $A$ is the midpoint of $C$ and $S$, which is the vertex.

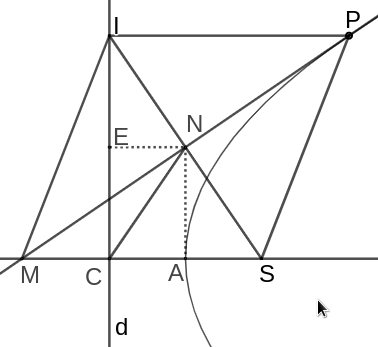
Now we can finally tick off the last goal.

[X] The perpendicular dropped from $N$ meets the axis of symmetry at the vertex.

And we're done! Having showed all four goals, we can now restate Newton's argument knowing that the proof is complete.

Since $MS = SP$, $MN = NP$, and $MA = AO$, then $\triangle MNS$ is congruent to $\triangle SNP$. The triangle $\triangle NAS$, by virtue of sharing $\angle NSA$ with $\triangle MNS$ and having a right angle at $\angle NAS$ is similar to $\triangle MNS$ and $\triangle SNP$. Therefore $PS$ is to $SN$, as $SN$ is to $NA$. This completes our proof of lemma XIV of Newton's Principia. Q.E.D.

In cyclic quadrilaterals, the angle between any side and a diagonal is equal to the angle between the opposite side and diagonal.

With many thanks to discord user NO MORE ALGEBRA for giving me crucial feedback on this writeup.